立体の観察、いろいろあるね!
小学5年の算数で、こんな問題がありました。
1辺が1㎝の立方体が集めて、下のような立体を作った。この立体の体積を求めなさい。
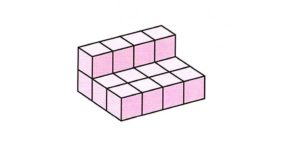
この問題を、A君は立方体を数えて、1㎤の立方体が16こあるので16㎤と答えました。もっともシンプルな考え方でしょうか。
Cさんは、立方体が4こ並んだ細長い棒(のようなもの)が4本あるので、4×4=16で16㎤と答えました。グループを作って観察するという方法です。
Mさんは、以下のような線を引いて、8×2=16で16㎤と答えました。同じ形で2つに分けるという方法ですが、向きが違うので「よく見つけたね!」という感じです。
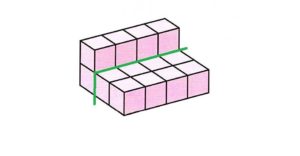
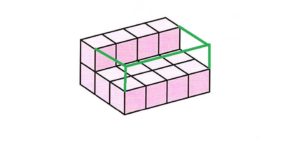
R君は、以下のように凹んでいる部分をいったん埋めて、
3×4×2=24
2×4×1=8
24-8=16
で16㎤としました。見えない線を引いて、世界を広げて考えるという工夫をしています。
一見、単純な問題のようですが、何の説明もせず(解法を示さず)考えさせると、いろいろな発想が出てくるものです。
物事をいろいろな角度から考察・検討することは極めて重要です。スタディクラブでは、メンバーに〇×だけでなく、プロセスを重視するようアドバイスし、その工夫に高い評価を伝えています。
僕はよくメンバーに「どうしてこういう答えになった?」「この考え方、説明して」と尋ねますが、予想外の回答が返ってくることもあり、非常に楽しい。
実のところ、上記のMさんの図形分割は、僕の頭の中にはなかった・・・。「すごいね!僕はこの解き方、思いつかなかったよ」と称賛。
こういうやりとりを繰り返していると、メンバーからの質問も途中の考え方を重視した、高度なものが混ざってきます。習慣は大切です。
メンバーと僕の双方向から思考を楽しむ … あらまほしきかな♪
